[Andrew ag] Dropout regularization
L2 정규화에 외에 또 다른 매우 강력한 정규화 기법은 드롭아웃입니다
어떻게 작동하는지 살펴봅시다
왼쪽처럼 과적합한 신경망을
훈련시키는 경우를 생각해봅시다
드롭아웃을 설명하기 위해
이 신경망의 복사본을 만들겠습니다
드롭아웃의 방식은
신경망의 각각의 층에 대해
노드를 삭제하는 확률을
설정하는 것입니다
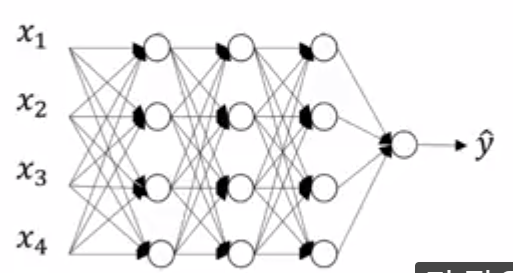

이 각각의 층에 대해
각각의 노드마다 동전을 던지면 0.5의 확률로 해당 노드를 유지하고 0.5의 확률로 노드를 삭제하게 됩니다
동전을 던진 후 다음과 같이 노드를 삭제했다고 해봅시다
그 후 삭제된 노드의 들어가는 링크와 나가는 링크를 모두 삭제합니다
그럼 더 작고 간소화된 네트워크가 됩니다
그럼 이 감소된 네트워크에서 하나의 샘플을 역전파로 훈련시킵니다
다른 샘플에 대해서도 동전을 던지고 다른 세트의 노드들을 남기고 다른 세트의 노드들은 삭제하게 됩니다
그럼 각각의 훈련 샘플에 대해서감소된 네트워크를 사용해
훈련시키게 됩니다
이것은 노드를 무작위로 삭제하는
이상한 기법처럼 보일수도 있습니다
그러나 실제로 잘 작동합니다
이것은 각각의 샘플에서 더 작은
네트워크를 훈련시키는 방식입니다
왜 네트워크를 정규화할 수 있는지에
대한 감을 얻을 수 있을 것입니다
더 작은 네트워크를
훈련시키기 때문입니다
드롭아웃을 어떻게 구현하는지 살펴봅시다
몇 가지 방법이 있습니다
역 드롭아웃이라고 불리는가장 일반적인 기법을 보여드리겠습니다
완전한 이해를 돕기 위해
층이 3인 경우를 예시로
나타내보도록 하겠습니다
층이 3인 경우에서
코드를 작성할 것입니다
단일 층에서 드롭아웃을 구현하는 방법을
확실하게 이해할 수 있을겁니다
먼저 층 3에 대한 드롭아웃 벡터인
벡터 d3를 설정합니다
np.random.rand
np.random.rand
a3와 같은 모양을 가지게 됩니다
이 값이 keep_prob이라는
숫자보다 작은지 비교합니다
keep_prob의 값은 이전 슬라이드에서는
0.5였지만 여기서는 0.8로 설정하겠습니다
이 수는 주어진 은닉 유닛이
유지될 확률입니다
keep_prob이 0.8이라는 것은
어떤 은닉 유닛이 삭제될 확률이
0.2라는 것입니다
어떤 은닉 유닛이 삭제될 확률이
0.2라는 것입니다
이 코드는 무작위의 행렬을
생성하게 됩니다
벡터화된 경우도 잘 실행됩니다
따라서 d3는 각각의 샘플과
각각의 은닉 유닛에 대해
0.8의 확률로
대응하는 d3가 1의 값을 가지고
0.2의 확률로 0의 값을 가지는
행렬이 될 것입니다
무작위의 숫자가
0.8보다 작을지의 여부는
0.8의 확률로 1이고,
즉 True가 되고
0.2보다 작을지의 여부는
0.2의 확률로 0, False가 됩니다
다음은 3번째 층의 활성화인
a3에 관한 코드를 작성하겠습니다
a3의 값은 예전 a3의 값에
요소별 곱셈으로
d3를 곱해준 것입니다
a3 *= d3로 써줘도 됩니다
모든 원소에 대해
20퍼센트의 확률로 0이 되는
d3의 원소를 곱해
대응되는 a3의 원소를
0으로 만들게 됩니다
이것을 파이썬으로 구현한다면
d3는 True와 False의 값을 갖는
불 타입의 행렬이 될 것입니다
그러나 0과 1이 아닌 불 타입의 값은
곱셈을 할 수 없게 됩니다
파이썬으로 구현하면
알게 될 것입니다
최종적으로 얻은 a3를
0.8로 나눠줍니다
keep_prob 매개변수로
나눠주는 것입니다
keep_prob 매개변수로
나눠주는 것입니다
이 마지막 단계에 대한
설명을 드리겠습니다
설명을 위해
세 번째 은닉 층에 50개의 유닛,
즉 50개의 뉴런이 있다고 해봅시다
그럼 a3는 (50, 1) 차원일 것입니다
벡터화한다면 (50, m) 차원입니다
80퍼센트의 확률로 유지하고
20퍼센트의 확률로 삭제한다면
평균적으로 10개의 유닛이
삭제된다는 뜻입니다
즉, 0의 값을 갖게 됩니다
z^[4]의 값을 살펴보면
w^[4]*a^[3]+b^[4]와 같습니다
w^[4]*a^[3]+b^[4]와 같습니다
w^[4]*a^[3]+b^[4]와 같습니다
예상대로 이 값은 20퍼센트만큼
줄어들 것입니다
즉 a^[3] 원소의 20퍼센트가
0이 된다는 의미입니다
z^[4]의 기대값을 줄이지 않기 위해
이 값을 0.8로 나눠줘야 합니다
이 값을 0.8로 나눠줘야 합니다
왜냐하면 필요한 20퍼센트 정도의 값을
다시 원래대로 만들 수 있기 때문입니다
이를 통해 a3의 기대값을
유지할 수 있습니다
따라서 여기 있는 이 줄이
역 드롭아웃이라고 불리는 기법입니다
keep_prob을 어떤 값으로 설정하든
0.8, 0.9, 1이든
1이면 값이 그대로 유지되니까
드롭아웃이 없는 것이네요
어쨌거나 keep_prob을 다시 나눠줌으로써
a3의 기대값을 같게 유지합니다
그리고 다음 슬라이드에서 살펴볼
신경망을 평가하는 경우에
이 역 드롭아웃 기법이
테스트를 쉽게 만들어줍니다
스케일링 문제가 적기 때문입니다
역 드롭아웃은 요즘 가장 보편적인
드롭아웃 기법이기도 합니다
이대로 구현하기를 추천드립니다
keep_prob으로 나누는 것을 빼고
훈련 반복을 하면
테스트할 때 알고리즘이
조금 더 복잡해집니다
그러나 사람들은 다른 버전은
잘 사용하지 않습니다
d 벡터를 사용해 서로 다른 훈련 샘플마다
다른 은닉 유닛들을 0으로 만들게 됩니다
같은 훈련 세트를 통해
여러 번 반복하면
그 반복마다 0이 되는 은닉 유닛은
무작위로 달라져야 합니다
따라서 하나의 샘플에서 계속 같은
은닉 유닛을 0으로 만드는 것이 아닌
경사 하강법의 하나의 반복마다
0이 되는 은닉 유닛들이 달라집니다
즉 같은 훈련 세트를
두 번째로 반복할 때는
0이 되는 은닉 유닛의 패턴이
달라지게 됩니다
세번째 층의 d3 벡터는
어떤 노드를 0으로 만들지 결정합니다
정방향 전파와 역전파 모두에서요
알고리즘의 훈련 후 테스트 시간에
하는 일을 말씀드리겠습니다
예측을 하고 싶은
x라는 샘플이 주어집니다
이 테스트 샘플인 x를 표현하기 위해
0 번째 층의 활성화 a^[0]를 사용하겠습니다
테스트에서는 드롭아웃을
사용하지 않습니다
그리고 z^[1]을
w^[1]a^[0]+b^[1]
a^[1] = g^[1](z^[1])
z^[2] = w^[2]a^[1]+b^[2]
z^[2] = w^[2]a^[1]+b^[2]
a^[2]도 같은 방식으로 설정합니다
마지막 층에 이르면 y의 예측값을 얻습니다
그러나 테스트에서는 명시적으로
드롭아웃을 사용하지 않기 때문에
어떤 은닉 유닛을 삭제할지에 관한
동전을 무작위로 던지지 않습니다
그 이유는 테스트에서는
예측을 하는 것이므로
결과가 무작위로 나오는 것을
원하지 않습니다
테스트에 드롭아웃을 구현하는 것은
노이즈만 증가시킬뿐입니다
이론적으로 무작위로 드롭아웃된
서로 다른 은닉 유닛을
예측 과정에서 여러 번 반복해
그들의 평균을 낼 수도 있지만
컴퓨터적으로 비효율적이고
이 과정과 거의 비슷한 결과를 냅니다
제가 이전 슬라이드에서 언급한
keep_prob으로 나누는
역 드롭아웃의 효과는
테스트에서 드롭아웃을 구현하지 않아도
활성화 기대값의
크기는 변하지 않기 때문에
테스트 할 때 스케일링 매개변수를
추가해주지 않아도 됩니다
여기까지 드롭아웃이었습니다
이번 주의 프로그래밍 과제에서
직접 구현해 볼 수 있을 겁니다
그러나 왜 드롭아웃이 실제로
잘 작동할까요?
다음 비디오에서 말씀드리죠